Esquema de los Números Reales: Guía Completa para Entender su Estructura

Introducción a los Números Reales

Los números reales son una parte fundamental de las matemáticas que nos rodean en la vida diaria. Desde contar el dinero que tenemos hasta medir el tiempo que nos toma llegar a un lugar, los números reales están en todas partes. Pero, ¿qué son exactamente? ¿Y cómo se estructuran? En este artículo, vamos a desglosar los números reales de una manera sencilla y accesible, para que puedas entender no solo su importancia, sino también cómo se relacionan entre sí. ¡Prepárate para un viaje fascinante a través del mundo de los números!

¿Qué son los Números Reales?

Los números reales son un conjunto de números que incluyen tanto los números racionales como los irracionales. Para ponerlo en términos más simples, los números racionales son aquellos que pueden expresarse como una fracción de dos enteros, como 1/2 o 3/4. Por otro lado, los números irracionales son aquellos que no pueden ser expresados de esta manera, como π (pi) o la raíz cuadrada de 2. Cuando juntamos estos dos grupos, obtenemos el conjunto completo de los números reales.

La Importancia de los Números Reales

Los números reales son cruciales en casi todas las áreas de las matemáticas y la ciencia. Imagina que estás construyendo una casa; necesitarás medir longitudes y áreas, y aquí es donde entran en juego los números reales. Sin ellos, no podríamos realizar cálculos precisos. Además, los números reales nos permiten modelar situaciones del mundo real, desde el crecimiento de poblaciones hasta la economía. En resumen, son la base sobre la cual se construyen muchas teorías y aplicaciones matemáticas.

Estructura de los Números Reales

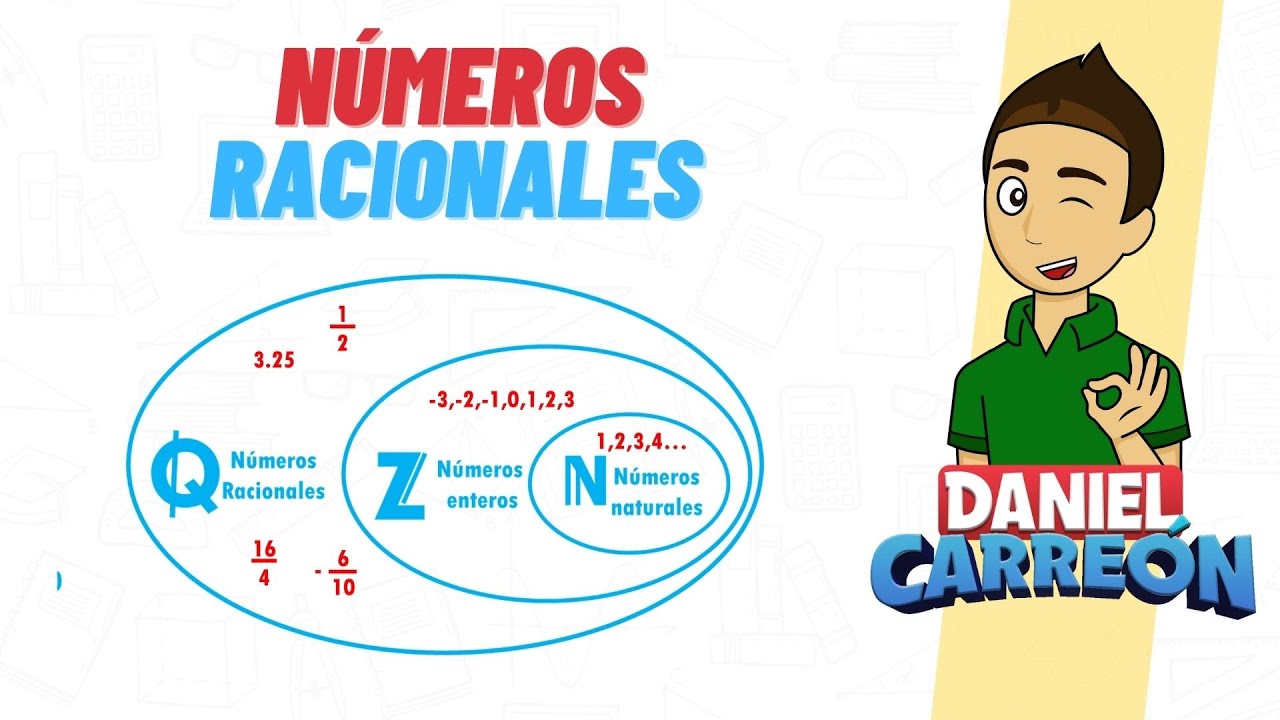
Para entender mejor los números reales, es útil visualizarlos como un vasto océano que contiene diferentes islas. Cada isla representa un subconjunto de números reales. Vamos a explorar estas «islas» y ver qué hay en cada una.

Números Naturales

Los números naturales son la primera isla que encontramos. Comienzan desde 1 y se extienden hacia el infinito: 1, 2, 3, 4, y así sucesivamente. Son los números que usamos para contar objetos, como el número de manzanas en una cesta. A menudo, se denotan con la letra N. Sin embargo, los números naturales no incluyen el cero ni los números negativos.

Números Enteros

La siguiente isla son los números enteros. Aquí, además de los números naturales, también encontramos sus opuestos, es decir, los números negativos: …, -3, -2, -1, 0, 1, 2, 3, … . Los enteros nos permiten realizar operaciones que involucran deudas o pérdidas. Por ejemplo, si tienes 5 manzanas y pierdes 2, puedes representarlo como 5 – 2 = 3.

Números Racionales

Ahora llegamos a la isla de los números racionales. Este conjunto incluye a todos los números que se pueden expresar como una fracción. Por ejemplo, 1/2, -3/4 y 5 son todos números racionales. Aquí, el 5 se puede escribir como 5/1. Este grupo es increíblemente útil porque nos permite realizar operaciones con números que no son enteros, como dividir una pizza entre varias personas.

Números Irracionales

Por último, pero no menos importante, tenemos los números irracionales. Esta isla es un poco más misteriosa, ya que sus habitantes no pueden ser expresados como fracciones. Un ejemplo famoso es π, que representa la relación entre la circunferencia de un círculo y su diámetro. La raíz cuadrada de 2 también es un número irracional, ya que su decimal es infinito y no periódico. Estos números son esenciales en matemáticas avanzadas y en muchas aplicaciones científicas.

Propiedades de los Números Reales

Los números reales tienen varias propiedades que los hacen únicos y útiles. Vamos a revisar algunas de las más importantes.

Cerradura

La propiedad de cerradura establece que si sumas o multiplicas dos números reales, el resultado siempre será otro número real. Por ejemplo, si tomas 2 y 3 (que son números reales) y los sumas, obtienes 5, que también es un número real. Esta propiedad es fundamental para la coherencia en las matemáticas.

Conmutatividad y Asociatividad

La conmutatividad y la asociatividad son propiedades que se aplican a la suma y la multiplicación. La conmutatividad nos dice que el orden no importa. Por ejemplo, 2 + 3 es lo mismo que 3 + 2. Por otro lado, la asociatividad implica que al sumar o multiplicar, no importa cómo agrupemos los números. Por ejemplo, (1 + 2) + 3 es lo mismo que 1 + (2 + 3).

Elemento Neutro

El elemento neutro es un número que, al ser sumado o multiplicado por otro número, no cambia el valor de este último. En la suma, el elemento neutro es 0, porque cualquier número sumado a 0 sigue siendo el mismo número. En la multiplicación, el elemento neutro es 1, ya que cualquier número multiplicado por 1 también sigue siendo el mismo.

Aplicaciones de los Números Reales

Los números reales no son solo un concepto teórico; tienen aplicaciones prácticas en la vida cotidiana. Vamos a explorar algunas de ellas.

En la Ciencia

En el ámbito científico, los números reales son fundamentales para realizar cálculos precisos. Por ejemplo, en la física, se utilizan para medir fuerzas, velocidades y energías. Sin los números reales, sería imposible describir fenómenos como la gravedad o la velocidad de la luz con precisión.

En la Economía

La economía también depende de los números reales. Desde calcular el interés de un préstamo hasta analizar las fluctuaciones del mercado, los economistas utilizan números reales para tomar decisiones informadas. Las gráficas y modelos económicos se basan en estos números para predecir tendencias y comportamientos del mercado.

En la Tecnología

En el mundo de la tecnología, los números reales son esenciales para el desarrollo de algoritmos y modelos computacionales. Por ejemplo, en la inteligencia artificial y el aprendizaje automático, se utilizan números reales para representar datos y realizar cálculos complejos. Sin ellos, no podríamos disfrutar de los avances tecnológicos que tenemos hoy en día.

Conclusión

Los números reales son un concepto fundamental en matemáticas y tienen un impacto significativo en nuestras vidas. Desde las operaciones más simples hasta las aplicaciones más complejas, su estructura y propiedades nos permiten entender y modelar el mundo que nos rodea. Ahora que tienes una comprensión más clara de los números reales, puedes apreciar su importancia en diversas disciplinas. ¿Te has preguntado alguna vez cómo se aplican en tu vida diaria? Desde medir la distancia hasta calcular tu presupuesto, los números reales son tus compañeros constantes.

Preguntas Frecuentes

• ¿Por qué los números irracionales son importantes? Los números irracionales son cruciales porque permiten una representación más completa de la realidad, especialmente en geometría y análisis matemático.
• ¿Cómo se utilizan los números reales en la vida cotidiana? Los números reales se utilizan en diversas situaciones, como al calcular el costo de una compra, medir distancias o realizar análisis financieros.
• ¿Los números reales son infinitos? Sí, el conjunto de los números reales es infinito, ya que siempre puedes encontrar un número entre dos números reales cualesquiera.
• ¿Qué es la recta numérica? La recta numérica es una representación visual de los números reales, donde cada punto en la línea representa un número real único.
• ¿Cómo se relacionan los números reales con otros conjuntos numéricos? Los números reales incluyen a los números naturales, enteros y racionales, además de los irracionales, formando un conjunto amplio y diverso.