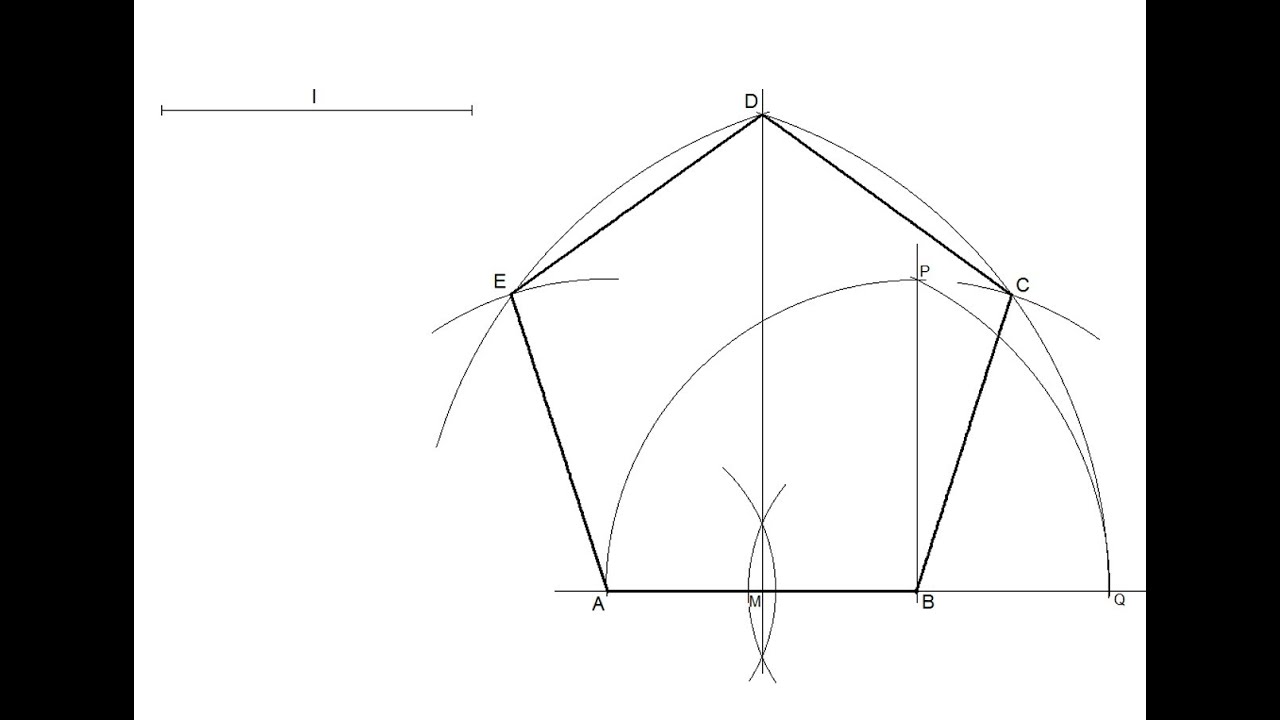
Cómo Calcular la Construcción de un Pentágono Dado el Lado: Guía Paso a Paso
Introducción al Mundo de los Pentágonos
¿Alguna vez te has preguntado cómo construir un pentágono perfecto solo conociendo la longitud de uno de sus lados? Si es así, estás en el lugar correcto. En esta guía paso a paso, vamos a desglosar el proceso de cálculo y construcción de un pentágono, una figura que no solo es fascinante por su forma, sino también por sus propiedades matemáticas y su presencia en la naturaleza y el arte. Así que, ponte cómodo y prepárate para sumergirte en el mundo de los pentágonos. Vamos a desmitificar esta figura geométrica de una manera sencilla y práctica.
¿Qué es un Pentágono?
Antes de entrar en los detalles de cómo calcular y construir un pentágono, es crucial entender qué es. Un pentágono es un polígono de cinco lados y cinco ángulos. Imagina que estás en una reunión de amigos, y cada uno de ellos representa un lado. Si todos están conectados, forman una figura cerrada: ¡un pentágono! La suma de sus ángulos interiores es de 540 grados, lo que significa que cada ángulo interior promedio mide 108 grados. Interesante, ¿verdad?
Materiales Necesarios
Para construir un pentágono, necesitarás algunos materiales básicos. No te preocupes, no se trata de un equipo de astronauta. Aquí tienes lo que necesitarás:
- Regla o cinta métrica
- Compás
- Lápiz
- Transportador (opcional, pero útil)
- Papela o cartón para el modelo
Con estos simples materiales, estarás listo para crear tu pentágono. Ahora, vamos a entrar en la parte divertida: ¡los cálculos!
Paso 1: Conocer la Longitud del Lado
El primer paso para construir tu pentágono es conocer la longitud de uno de sus lados. Supongamos que decides que cada lado medirá 5 cm. Este es tu punto de partida. Recuerda, la longitud de los lados es esencial para que tu pentágono tenga la forma correcta. Sin esta medida, estarías tratando de construir una casa sin planos, ¡y eso no suena muy divertido!
Paso 2: Calcular la Distancia desde el Centro
Una vez que tienes la longitud del lado, el siguiente paso es calcular la distancia desde el centro del pentágono hasta uno de sus vértices, lo que se conoce como el «radio» del pentágono. Esta distancia se puede calcular usando la siguiente fórmula:
Radio (r) = Lado / (2 * sin(π/5))
Donde «Lado» es la longitud que elegiste. Para nuestro ejemplo de 5 cm, el cálculo sería:
r = 5 / (2 * sin(π/5)) ≈ 5 / (2 * 0.5878) ≈ 4.25 cm
Esto significa que el radio del pentágono es aproximadamente 4.25 cm. ¿Ves cómo las matemáticas comienzan a tomar forma? ¡Ya estamos más cerca de nuestro objetivo!
Paso 3: Dibujar el Círculo
Ahora que conoces el radio, es hora de usar el compás. Coloca la punta del compás en el punto donde deseas que esté el centro de tu pentágono y ajusta la otra parte a la longitud del radio que calculaste (4.25 cm). Dibuja un círculo. Este círculo será tu guía para colocar los vértices del pentágono.
Imagina que estás dibujando una pizza, donde el centro es la parte más deliciosa y cada porción representa un lado del pentágono. ¡Es hora de cortar esa pizza!
Paso 4: Dividir el Círculo en Cinco Partes Iguales
Ahora, necesitamos marcar los cinco vértices del pentágono en el círculo. Para ello, puedes usar el transportador o simplemente calcular los ángulos. Cada ángulo debe ser de 72 grados (360 grados / 5 lados). Así que, desde un punto en el círculo, mide 72 grados y marca el primer vértice. Repite este proceso hasta que tengas los cinco puntos marcados en el círculo.
Consejos para una Medición Precisa
Si no tienes un transportador, no te preocupes. Puedes usar la regla para medir la distancia entre los puntos en el círculo. La clave es que los cinco vértices estén equidistantes. ¡Tu pentágono empezará a tomar forma!
Paso 5: Conectar los Vértices
Ahora viene la parte emocionante: conectar los puntos. Utiliza tu regla para dibujar líneas rectas entre cada uno de los cinco vértices. Esto formará el contorno de tu pentágono. Si has hecho todo correctamente, deberías tener una figura que se ve equilibrada y simétrica. ¡Mira cómo cobra vida tu creación!
Paso 6: Ajustes y Revisión
Es posible que desees revisar las medidas y ajustar algunas líneas para asegurarte de que todo esté alineado. Si algo no se ve bien, no dudes en hacer correcciones. La perfección está en los detalles, y un pequeño ajuste puede hacer una gran diferencia. A veces, el arte se trata de hacer ajustes hasta que todo se sienta justo.
¿Qué Hacer Después de Construir tu Pentágono?
Una vez que hayas completado tu pentágono, puedes decorarlo, colorearlo o incluso usarlo como base para un proyecto más grande. La geometría está presente en muchas áreas de la vida, desde la arquitectura hasta el diseño gráfico. Así que, ¿por qué no aprovechar tu nuevo conocimiento y crear algo asombroso?
Preguntas Frecuentes
¿Puedo construir un pentágono con lados de diferentes longitudes?
No, un pentágono regular tiene todos sus lados y ángulos iguales. Si deseas un pentágono irregular, puedes jugar con diferentes longitudes, pero eso requerirá un enfoque diferente en los cálculos.
¿Dónde se utilizan los pentágonos en la vida real?
Los pentágonos aparecen en diversas áreas, desde la arquitectura hasta el arte. Un ejemplo famoso es el Pentágono en Washington D.C., que es un edificio en forma de pentágono que alberga el Departamento de Defensa de los Estados Unidos.
¿Es difícil construir un pentágono?
No es difícil una vez que entiendes los pasos. Al principio puede parecer complicado, pero con un poco de práctica, te volverás un experto en la construcción de pentágonos.
¿Qué otras formas geométricas puedo aprender a construir?
Existen muchas formas geométricas fascinantes, como triángulos, cuadrados, hexágonos y más. Cada una tiene sus propias propiedades y métodos de construcción, ¡así que sigue explorando!
Así que ahí lo tienes, una guía completa para calcular y construir un pentágono dado el lado. Espero que hayas disfrutado el proceso tanto como yo. ¡Ahora sal y crea tus propias maravillas geométricas!